#94 Suppose the field inside a large piece of dielectric
Suppose the field inside a large piece of dielectric - physics
Chemistry Explain daily providing Q&A content “#94 Suppose the field inside a large piece of dielectric" in physics, Advent physical therapy, Agile physical therapy, Allied physical therapy.Get the Free Online Chemistry Q&A Questions And Answers with explain. To crack any examinations and Interview tests these Chemistry Questions And Answers are very useful. Here we have uploaded the Free Online Chemistry Questions. Here we are also given the all chemistry topic.
Chemistry Explain team has covered all Topics related to inorganic, organic, physical chemistry, and others So, Prepare these Chemistry Questions and Answers with Explanation Pdf.
For More Chegg Questions
Free Chegg Question
Suppose the field inside a large piece of the dielectric is E0, so that the electric displacement is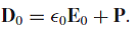
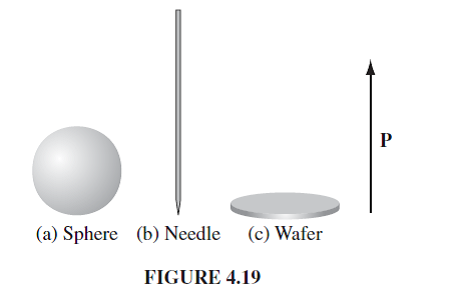
(a) Now a small spherical cavity (Fig. 4.19a) is hollowed out of the material. Find the field at the center of the cavity in terms of E0 and P. Also find the displacement at the center of the cavity in terms of D0 and P. Assume the polarization is âfrozen in,â so it doesnât change when the cavity is excavated.
(b) Do the same for a long needle-shaped cavity running parallel to P (Fig. 4.19b).
(c) Do the same for a thin wafer-shaped cavity perpendicular to P (Fig. 4.19c). Assume the cavities are small enough that P, E0, and D0 are essentially uniform. [Hint: Carving out a cavity is the same as superimposing an object of the same shape but opposite polarization.]
Figure 4.19
For More Chemistry Notes and Helpful Content Subscribe Our YouTube Chanel - Chemistry Explain
Free Chegg Answer
Electric displacement is a topic discussed in electromagnetism that measures the response of dielectric insulating materials that applies to the electric field. A conducting material remains neutral before applying an electric field on it. It means there is no movement in charge of particles inside the material.
When electric field is applied to the material, the free charges start responding to the force of field. The whole material becomes polarized as because the positive charges shift towards the direction of the applied field (electric) and the negative charges move in the opposite direction of the electric field. Thus, polarization P takes place within the material.

Here, is the dielectric field.
is the dielectric field.
So, Displacement is defined as follows:

When electric field is applied to the material, the free charges start responding to the force of field. The whole material becomes polarized as because the positive charges shift towards the direction of the applied field (electric) and the negative charges move in the opposite direction of the electric field. Thus, polarization P takes place within the material.

Here,
 is the dielectric field.
is the dielectric field.So, Displacement is defined as follows:

(a)
From Gaussâs law, it is found that surface integral of displacement current is

Here, is the charge is enclosed on the surface and is the small area.
is the charge is enclosed on the surface and is the small area.
We know, field due to electricity inside a uniformly polarised sphere is,
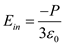 â¦â¦ (1)
â¦â¦ (1)
Here, is permittivity in free space.
is permittivity in free space.
If is the electric field inside the dielectric material, then total field at the center inside the cavity is
is the electric field inside the dielectric material, then total field at the center inside the cavity is  â¦â¦ (2)
â¦â¦ (2)
From equation (1) and (2) we get,
 â¦.. (3)
â¦.. (3)
From Maxwellâs differential equation,
Electric displacement,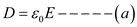
Substituting the value of E from equation (3), in (a)

Therefore,
 â¦â¦ (4)
â¦â¦ (4)
We know, electric field displacement

Substituting in equation (4),
in equation (4),

From Gaussâs law, it is found that surface integral of displacement current is

Here,
 is the charge is enclosed on the surface and is the small area.
is the charge is enclosed on the surface and is the small area.We know, field due to electricity inside a uniformly polarised sphere is,
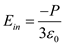 â¦â¦ (1)
â¦â¦ (1)Here,
 is permittivity in free space.
is permittivity in free space.If
 is the electric field inside the dielectric material, then total field at the center inside the cavity is
is the electric field inside the dielectric material, then total field at the center inside the cavity is  â¦â¦ (2)
â¦â¦ (2)From equation (1) and (2) we get,
 â¦.. (3)
â¦.. (3)From Maxwellâs differential equation,
Electric displacement,
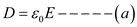
Substituting the value of E from equation (3), in (a)

Therefore,
 â¦â¦ (4)
â¦â¦ (4)We know, electric field displacement

Substituting
 in equation (4),
in equation (4),
(b)
The electric field inside the cavity of the needle
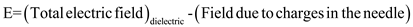
In the above equation, the field due to charges is negligible due to a very small magnitude.
So, we can write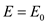 .
.
Thus, it can be said that the electric field inside the cavity (needle-shaped) is equal to the electric field due to dielectric.
But we know that,

Therefore,
 â¦â¦ (5)
â¦â¦ (5)
From the electric field displacement equation, .
.
Now substituting the above value in equation (5)

The electric field inside the cavity of the needle
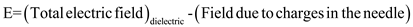
In the above equation, the field due to charges is negligible due to a very small magnitude.
So, we can write
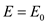 .
.Thus, it can be said that the electric field inside the cavity (needle-shaped) is equal to the electric field due to dielectric.
But we know that,

Therefore,
 â¦â¦ (5)
â¦â¦ (5)From the electric field displacement equation,
 .
.Now substituting the above value in equation (5)

Thus, the electric displacement that parallels to the needle with cavity shape is 

(c)
The electric field due to the cavity is

Therefore,
 â¦â¦ (6)
â¦â¦ (6)
From Maxwellâs equation, .
.
From equation (6), substituting the value of E in D,

Thus,
 â¦â¦ (7)
â¦â¦ (7)
But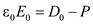
Substituting the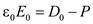 in equation (7),
in equation (7),

Hence, the electric displacement which is parallel to the thin cavity (with wafer shape).
The electric field due to the cavity is

Therefore,
 â¦â¦ (6)
â¦â¦ (6)From Maxwellâs equation,
 .
.From equation (6), substituting the value of E in D,

Thus,
 â¦â¦ (7)
â¦â¦ (7)But
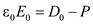
Substituting the
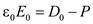 in equation (7),
in equation (7),
Hence, the electric displacement which is parallel to the thin cavity (with wafer shape).
Labels: Chegg, Free Chegg Answer, Q&A Physics


0 Comments:
Post a Comment
Subscribe to Post Comments [Atom]
<< Home