#601 The concrete specific weight 150 lb/ft3 seawall
The concrete specific weight of 150 lb/ft3 seawall - Mechanical Engineering
ChemistryExplain daily providing Q&A content “#601 The concrete specific weight 150 lb/ft3 seawall" in Mechanical Engineering, Best colleges for mechanical engineering, Entry level mechanical engineer, Mechanical engineering companies
Get the Free Online Chemistry Q&A Questions And Answers with explain. To crack any examinations and Interview tests these Chemistry Questions And Answers are very useful. Here we have uploaded the Free Online Chemistry Questions. Here we are also given the all chemistry topic.
ChemistryExplain team has covered all Topics related to inorganic, organic, physical chemistry, and others So, Prepare these Chemistry Questions and Answers with Explanation Pdf.
For More Chegg Questions
Join Our Telegram Channel for Covers All Update by ChemistryExplain:- Click Now
Free Chegg Question
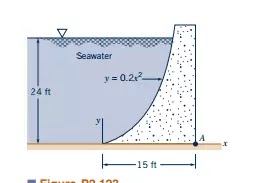
The concrete (specific weight 150 lb/ft3 ) seawall of Fig. P2.123 has a curved surface and restrains seawater at a depth of 24 ft. The trace of the surface is a parabola as illustrated. Determine the moment of the fluid force (per unit length) with respect to an axis through the toe (point A).
Free Chegg AnswerFor More Chemistry Notes and Helpful Content Subscribe Our YouTube Chanel - Chemistry Explain
Free Chegg Answer
General guidance
When the surface is submerged in a fluid, the forces developed on the surface due to the fluid.
Calculation of these forces is an important role in design of tanks, dams, and hydraulic structures.
Force must be perpendicular to the surface for static fluids since no shear stresses are involved.
Write the formula for hydrostatic force.
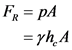
Here, the specific weight of fluid is 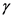 , area of the dam is A and centroidal distance of dam is hc.
, area of the dam is A and centroidal distance of dam is hc.
Write the formula for weight of the dam.
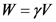
Here, the volume of the fluid is 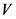 .
.
Write the formula for a moment.
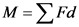
Step 1 of 6
Draw the free-body diagram of the system when it has turned through an angle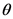 .
.
Hydrostatic force is F1 and weight is W.
Step 2 of 6
Compute the horizontal component of fluid force acting on the wall.
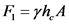
Here, 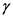 is the weight density of the fluid,
is the weight density of the fluid, 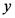 is the height at which the horizontal component acts and
is the height at which the horizontal component acts and 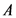 is the projected vertical area on which the force acts h the height of the sea wall and l the length of the sea wall.
is the projected vertical area on which the force acts h the height of the sea wall and l the length of the sea wall.
Substitute 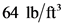 for
for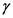 ,
, 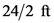 for
for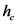 ,
, 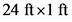 for
for  (since unit length).
(since unit length).
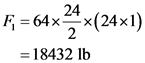
Use hydrostatic force formula to find horizontal components of fluid force.
Step 3 of 6
Draw the curved section of the concrete wall.
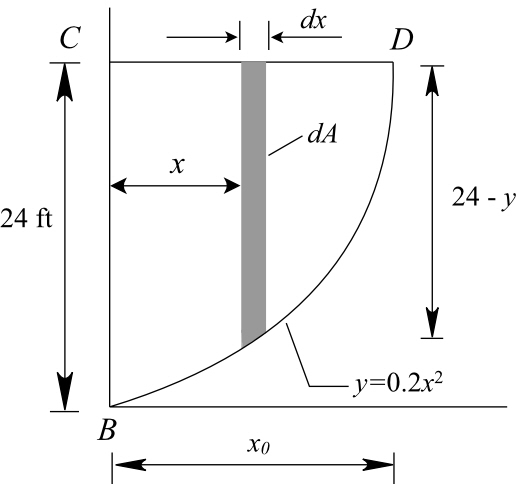
Use a strip diagram to find the area of the wall.
Step 4 of 6
Calculate the value of 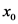 using the curve equation.
using the curve equation.
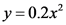 …… (1)
…… (1)
Substitute, 24 ft for y.
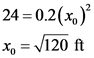
Determine the area of BCD.
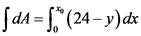 …… (2)
…… (2)
Substitute equation (1) in equation (2).
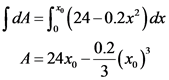
Substitute 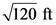 for
for 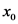 .
.
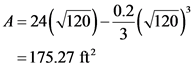
Use integration relation of the curve to find the area of the wall.
Step 5 of 6
Calculate the vertical force acting on the concrete wall.
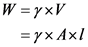
Substitute 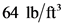 for
for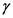 ,
, 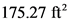 for A, and
for A, and 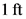 for l (since unit length).
for l (since unit length).
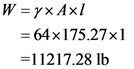
Calculate the centroid of the area.
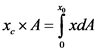
Here, the distance of the centroid from the y-axis is 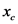 and the area of the section is A.
and the area of the section is A.
Substitute 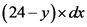 for
for 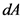 and
and 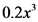 for
for 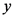 .
.
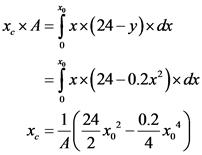
Substitute 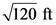 for
for 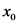 and
and 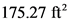 for A.
for A.
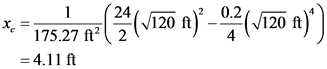
Use the weight of dam relation and centroid relation to finding the vertical force on the dam and distance of the centroid from the y-axis.
Step 6 of 6
Calculate the moment of the fluid about point A.
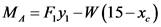
Here, the distance of centroid of the parabolic section from the x-axis is 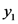
Substitute 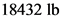 for
for 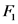 ,
, 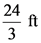 for
for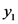 ,
, 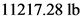 for W, and
for W, and 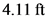 for
for 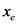 .
.
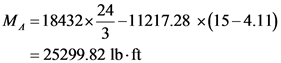
Therefore, the moment about point A is 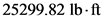 .
.
Explanation
Consider vertical force and hydrostatic forces on the dam to find the moment about point A.
Answer
Therefore, the moment about point A is 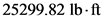 .
.
Labels: Chegg, Free Chegg Answer, Q&A Mechanical Engineering


0 Comments:
Post a Comment
Subscribe to Post Comments [Atom]
<< Home