#493 The magnitude of the net force exerted

The magnitude of the net force exerted - Physics

ChemistryExplain daily providing Q&A content “#493 The magnitude of the net force exerted" in Physics, Ap physics 1 practice test, Best colleges for physics, Best physics books, Best physics schools

Get the Free Online Chemistry Q&A Questions And Answers with explain. To crack any examinations and Interview tests these Chemistry Questions And Answers are very useful. Here we have uploaded the Free Online Chemistry Questions. Here we are also given the all chemistry topic.

 ChemistryExplain team has covered all Topics related to inorganic, organic, physical chemistry, and others So, Prepare these Chemistry Questions and Answers with Explanation Pdf.

For More Chegg Questions

• Inorganic Chemistry
• Organic Chemistry
• Physical Chemistry

Free Chegg Question

The magnitude of the net force exerted in the x direction on a 3.90-kg particle varies in time as shown in the figure below.

(a) Find the impulse of the force over the 5.00-s time interval. I = ? (N · s)

(b) Find the final velocity the particle attains if it is originally at rest. Vf = ? (m/s)

(c) Find its final velocity if its original velocity is -3.10 i m/s. Vf = ? (m/s)

(d) Find the average force exerted on the particle for the time interval between 0 and 5.00 s. Favg = ? (N)

Free Chegg AnswerFor More Chemistry Notes and Helpful Content Subscribe Our YouTube Chanel - Chemistry Explain  

Free Chegg Answer

General guidance

Concepts and reason

The concepts used to solve this question is the impulse

Initially, draw the graph and then the impulse is determined by calculating the area under the graph. Later use the impulse to find the initial and final velocities of the particle. At last use the relation between impulse, force and time to determine average force acting on the particle.

Fundamentals

Impulse:

Impulse is a vector quantity and has both magnitudes as well as direction. It is defined as the product of the force acting on the particle and time interval at which force is acting on the particle.

The magnitude of the impulse is,

$I=F\Delta t$

Here, $F$ is the force acting on the particle and $\Delta t$ is the time interval.

The impulse is also defined as the change in momentum of the particle.

$I=m\Delta v$

Here, $m$ is the mass of the particle and $\Delta v$ is the change in velocity.

Step 1 of 4

(a)

The graph between the force and the time is drawn below.

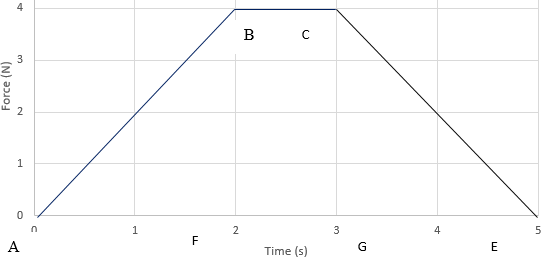
The area of the graph gives the impulse.

Therefore,

I=Area(ABF)+Area(BCFG)+Area(CEG)=(21​)(4N)(2s)+(4N)(1s)+(21​)(4N)(2s)=2(4N⋅s)+4N⋅s=12N⋅s​

Part a

The impulse of the force over the time interval $5\mathbf{s}$ is $12\mathrm{N}\cdot \mathrm{s}$

Explanation | Common mistakes | Hint for next step

The area under the graph gives the impulse. The units of the impulse is $\mathrm{N}\cdot \mathrm{s}$ . The area of the graph is formed by two triangles and one rectangle. The total area of the graph is the sum of the area of two triangles and one rectangle.

Step 2 of 4

(b)

The final velocity of the particle is,

I=m(vf​−vi​)

The above equation is modified as,

vf​=mI​+vi​ …… (1)

Here, vi​ is the initial velocity of the particle.

Substitute $12\mathrm{N}\cdot \mathrm{s}$ for $I$ , $3.90\mathrm{k}\mathrm{g}$ for $m$ and $0\mathrm{m}/\mathrm{s}$ for vi​ in the equation (1).

vf​=mI​+vi​=3.90kg12N⋅s​+0m/s=3.076m/s​

Part b

The final velocity of the particle is $3.076\mathbf{m}/\mathbf{s}$

Explanation | Common mistakes | Hint for next step

The particle starts from rest and therefore the initial velocity of the particle is zero. Hence, the final velocity of the particle depends on the impulse and mass of the particle.

Step 3 of 4

(c)

The final velocity of the particle is,

vf​=mI​+vi​ …… (2)

Here, vi​ is the initial velocity of the particle.

Substitute $12\mathrm{N}\cdot \mathrm{s}$ for $I$ , $3.90\mathrm{k}\mathrm{g}$ for $m$ and $-3.10\mathrm{m}/\mathrm{s}$ for vi​ in the equation (2).

vf​=mI​+vi​=3.90kg12N⋅s​−3.10m/s=−0.024m/s​

Part c

The final velocity of the particle is $-0$.024m/s

Explanation | Common mistakes | Hint for next step

The initial velocity of the particle is known and therefore by using the impulse equation, the final velocity of the particle has been determined.

Step 4 of 4

(d)

The average force exerted on the particle is,

F=ΔtI​ …… (3)

Substitute $12\mathrm{N}\cdot \mathrm{s}$ for $I$ and $5\mathrm{s}$ for $\Delta t$ in the equation (3).

F=ΔtI​=5s12N⋅s​=2.4N​

Part d

The average force exerted on the particle is $2.4\mathbf{N}$

Explanation | Common mistakes

The force acting on the particle is,

$F\propto I$

And,

F∝Δt1​

Hence, from the above relations, the average force acting on the particle is directly proportional to the impulse. Hence, with an increase in the impulse, the average force exerted on the particle will increase.

Answer

Part a

The impulse of the force over the time interval $5\mathbf{s}$ is $12\mathrm{N}\cdot \mathrm{s}$

Part b

The final velocity of the particle is $3.076\mathbf{m}/\mathbf{s}$

Part c

The final velocity of the particle is $-0$.024m/s

Part d

The average force exerted on the particle is $2.4\mathbf{N}$