#435 A beam supports three loads of given
A beam supports three loads of given - Mechanical Engineering
ChemistryExplain daily providing Q&A content “#435 A beam supports three loads of given" in Mechanical Engineering, Best colleges for mechanical engineering, Entry level mechanical engineer, Mechanical engineering companies
Get the Free Online Chemistry Q&A Questions And Answers with explain. To crack any examinations and Interview tests these Chemistry Questions And Answers are very useful. Here we have uploaded the Free Online Chemistry Questions. Here we are also given the all chemistry topic.
ChemistryExplain team has covered all Topics related to inorganic, organic, physical chemistry, and others So, Prepare these Chemistry Questions and Answers with Explanation Pdf.
For More Chegg Questions
Free Chegg Question
A beam supports three loads of given magnitude and a fourth load whose magnitude is a function of position. If b = 1.5 m and the loads are to be replaced with a single equivalent force, determine (a) the value of a so that the distance from support A to the line of action of the equivalent force is maximum,(b) the magnitude of the equivalent force and its point of application on the beam.
Free Chegg AnswerFor More Chemistry Notes and Helpful Content Subscribe Our YouTube Chanel - Chemistry Explain
Free Chegg Answer
-
Step 1 of 8
-
Step 2 of 8
Given
The distance,
Let
be the single equivalent force acting on the beam and
be the distance from end A where the force
is acting
We have,
-
Step 3 of 8
Take the moment about the point A. Take sign conventions; anti-clockwise moments are taken as positive
-
Step 4 of 8
Now, simplify
----- (2)
-
Step 5 of 8
a) Find the value of a to maximize L. Now, take the derivative of L with respect to a.
-
Step 6 of 8
Now, we have
Now, solve the expression.
Since
, a must be less than 9 m
Therefore, the distance is
-
Step 7 of 8
b) Substitute the value of a in equation (1) and solve
Therefore, the equivalent force is
-
Step 8 of 8
Substitute the value of a in equation (2) and solve
Labels: Chegg, Free Chegg Answer, Q&A Mechanical Engineering





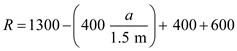


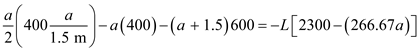







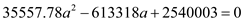


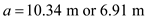








0 Comments:
Post a Comment
Subscribe to Post Comments [Atom]
<< Home