#102 Forces are applied at points A and B of the solid cast-iron
Forces are applied at points A and B of the solid cast-iron - Mechanical Engineering
ChemistryExplain daily providing Q&A content “#102 Forces are applied at points A and B of the solid cast-iron" in Mechanical Engineering, Best colleges for mechanical engineering, Entry level mechanical engineer, Mechanical engineering companies.Get the Free Online Chemistry Q&A Questions And Answers with explain. To crack any examinations and Interview tests these Chemistry Questions And Answers are very useful. Here we have uploaded the Free Online Chemistry Questions. Here we are also given the all chemistry topic.
ChemistryExplain team has covered all Topics related to inorganic, organic, physical chemistry, and others So, Prepare these Chemistry Questions and Answers with Explanation Pdf.
For More Chegg Questions
Free Chegg Question
Forces are applied at points A and B of the solid cast-iron bracket shown. Knowing that the bracket has a diameter of 0.8 in., determine the principal stresses and the maximum shearing stress at (a) point H, (b) point K.For More Chemistry Notes and Helpful Content Subscribe Our YouTube Chanel - Chemistry Explain
Free Chegg Answer
Draw the free-body diagram of the solid cast iron:
Forces Couples
Forces Couples
Find the force in Z-direction from the diagram
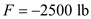
Find the force in y-direction from the diagram
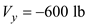
Find the moment in x-direction from the diagram
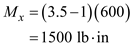
Find the moment in y-direction from the diagram
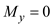
Find the moment in z-direction from the diagram
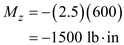
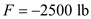
Find the force in y-direction from the diagram
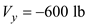
Find the moment in x-direction from the diagram
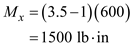
Find the moment in y-direction from the diagram
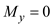
Find the moment in z-direction from the diagram
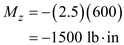
Find the radius of a bracket by using geometric properties of the section
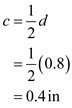
Here, the diameter of the bracket is d
Find the area bracket by using the equation
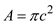
Substitute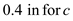 in the above equation
in the above equation
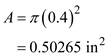
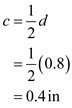
Here, the diameter of the bracket is d
Find the area bracket by using the equation
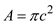
Substitute
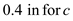 in the above equation
in the above equation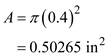
Find the moment of inertia by using the equation
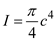
Substitute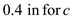 in the above equation
in the above equation
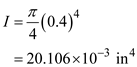
Find the polar moment of inertia by using the equation
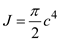
Substitute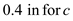 in the above equation
in the above equation
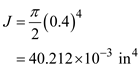
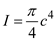
Substitute
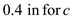 in the above equation
in the above equation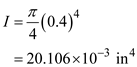
Find the polar moment of inertia by using the equation
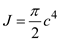
Substitute
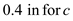 in the above equation
in the above equation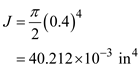
Determine the first moment Q by using the equation
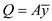
Here, the centroid of the semicircle
Substitute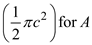
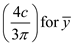 in the above equation
in the above equation
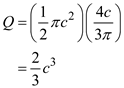
Substitute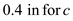 in the above equation
in the above equation
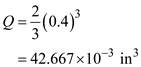
Find the thickness by using the equation
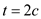
Substitute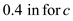 in the above equation
in the above equation
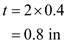
(a)
Find the bending stresses at point H by using the equation
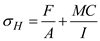
Substitute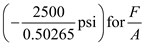 and
and 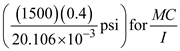 in the above equation
in the above equation

Find the maximum shearing stress at point H by using the equation
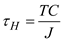
Substitute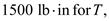
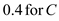 and
and 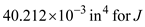 in the above equation
in the above equation
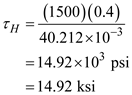
Find the average stress by using the equation
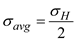
Substitute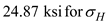 in the above equation
in the above equation
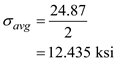
Find the radius of the circle by using the equation
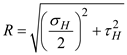
Substitute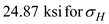 and
and 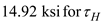 in the above equation
in the above equation
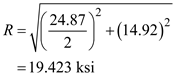
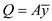
Here, the centroid of the semicircle
Substitute
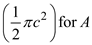
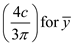 in the above equation
in the above equation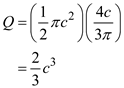
Substitute
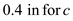 in the above equation
in the above equation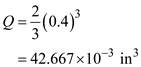
Find the thickness by using the equation
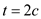
Substitute
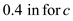 in the above equation
in the above equation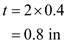
(a)
Find the bending stresses at point H by using the equation
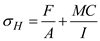
Substitute
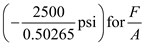 and
and 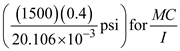 in the above equation
in the above equation
Find the maximum shearing stress at point H by using the equation
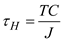
Substitute
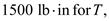
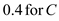 and
and 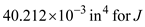 in the above equation
in the above equation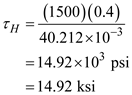
Find the average stress by using the equation
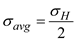
Substitute
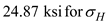 in the above equation
in the above equation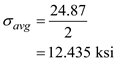
Find the radius of the circle by using the equation
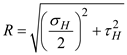
Substitute
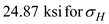 and
and 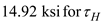 in the above equation
in the above equation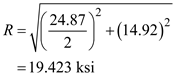
Find the maximum principle stress by using the equation at point H
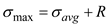
Substitute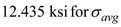 and
and 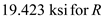

Therefore, the maximum principal stress at point H is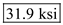
Find the minimum principle stress by using the equation at point H
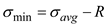
Substitute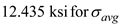 and
and 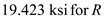

Therefore, the minimum principal stress at point H is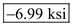
Find the maximum shear stress at point H
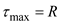
Substitute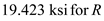 in the above equation
in the above equation
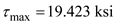
Therefore, the maximum shear stress at point H is
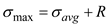
Substitute
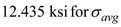 and
and 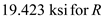

Therefore, the maximum principal stress at point H is
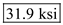
Find the minimum principle stress by using the equation at point H
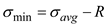
Substitute
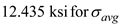 and
and 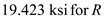

Therefore, the minimum principal stress at point H is
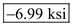
Find the maximum shear stress at point H
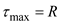
Substitute
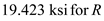 in the above equation
in the above equation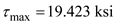
Therefore, the maximum shear stress at point H is

(b)
Find the stress at point K by using the equation
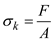
Substitute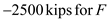 and
and 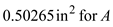 in the above equation
in the above equation

Find the shear stress at point K by using the equation
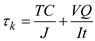
Substitute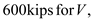
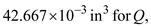
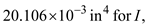
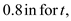
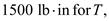
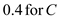 and
and 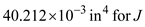 in the above equation
in the above equation
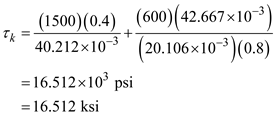
Find the average stress by using the equation at point K
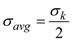
Substitute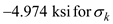 in the above equation
in the above equation
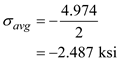
Find the radius of the circle by using the equation at point K
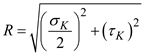
Substitute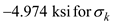 and
and 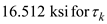 in the above equation
in the above equation
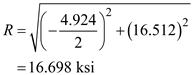
Find the stress at point K by using the equation
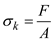
Substitute
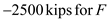 and
and 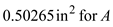 in the above equation
in the above equation
Find the shear stress at point K by using the equation
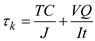
Substitute
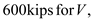
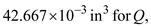
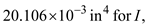
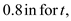
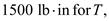
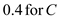 and
and 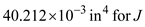 in the above equation
in the above equation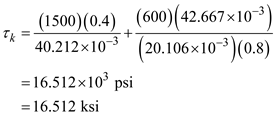
Find the average stress by using the equation at point K
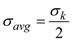
Substitute
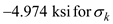 in the above equation
in the above equation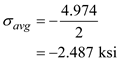
Find the radius of the circle by using the equation at point K
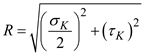
Substitute
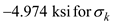 and
and 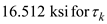 in the above equation
in the above equation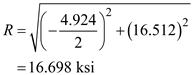
Find the maximum stress by using the equation at point K
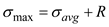
Substitute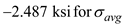 and
and 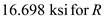 in the above equation
in the above equation

Therefore, the maximum principal stress at point K is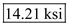
Find the minimum stress by using the equation at point K
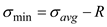
Substitute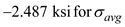 and
and 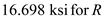 in the above equation
in the above equation
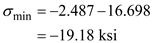
Therefore, the minimum principal stress at point K is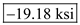
Find the maximum shear stress by using the equation at point K
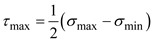
Substitute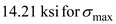 and
and 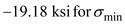 in the above equation
in the above equation

Therefore, the maximum shear stress at point K is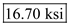
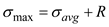
Substitute
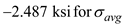 and
and 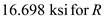 in the above equation
in the above equation
Therefore, the maximum principal stress at point K is
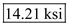
Find the minimum stress by using the equation at point K
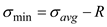
Substitute
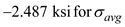 and
and 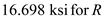 in the above equation
in the above equation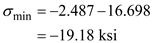
Therefore, the minimum principal stress at point K is
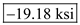
Find the maximum shear stress by using the equation at point K
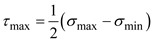
Substitute
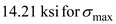 and
and 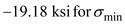 in the above equation
in the above equation
Therefore, the maximum shear stress at point K is
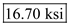
Labels: Chegg, Free Chegg Answer, Q&A Mechanical Engineering




0 Comments:
Post a Comment
Subscribe to Post Comments [Atom]
<< Home