Tuesday, August 4, 2020

#107 Generating Functions and Labelled Graphs

Generating Functions and Labelled Graphs - Math

ChemistryExplain daily providing Q&A content “#107 Generating Functions and Labelled Graphs" in Bridges math curriculum, Dr mather, Carnegie math, 10th maths, 10th-grade math problems, Math
ChemistryExplain “#107 Generating Functions and Labelled Graphs in Bridges math curriculum, Dr mather, Carnegie math, 10th maths, 10th-grade math problems, Math
Get the Free Online Chemistry Q&A Questions And Answers with explain. To crack any examinations and Interview tests these Chemistry Questions And Answers are very useful. Here we have uploaded the Free Online Chemistry Questions. Here we are also given the all chemistry topic.
 ChemistryExplain team has covered all Topics related to inorganic, organic, physical chemistry, and others So, Prepare these Chemistry Questions and Answers with Explanation Pdf.
For More Chegg Questions

Free Chegg Question

Generating Functions and Labelled Graphs
ChemistryExplain “#107 Generating Functions and Labelled Graphs in Bridges math curriculum, Dr mather, Carnegie math, 10th maths, 10th-grade math problems, Math
Note, a consequence of the definition is that two labelled graphs can be isomorphic as graphs, but still be different labelled graphs.
Let F(x) and (x) be the exponential generating series for the number of labelled graphs and the number of connected graphs, respectively. In other words:
ChemistryExplain “#107 Generating Functions and Labelled Graphs in Bridges math curriculum, Dr mather, Carnegie math, 10th maths, 10th-grade math problems, Math
where an is the number of labelled graphs with n vertices, and by is the number of connected labelled graphs with n vertices.
ChemistryExplain “#107 Generating Functions and Labelled Graphs in Bridges math curriculum, Dr mather, Carnegie math, 10th maths, 10th-grade math problems, Math
For More Chemistry Notes and Helpful Content Subscribe Our YouTube Chanel - Chemistry Explain  

Free Chegg Answer

1. Since a_n is the number of labelled graphs on n vertices, we have
an no. of ECP2([n]) = 2P2([n]) = 2()
2. We prove via induction on m that H(x)^m/m! is the exponential generating series for labeled graph with exactly m connected components.
When m=1 , this is just the definition of H(x)^1/1!=H(x) .
Suppose this is true for some m\geq 1 . Let G=([n],E) be a graph with m+1 connected components, and write its generating series as
k_{m+1}(x)=\sum_{n=1}^\infty c_n\frac {x^n}{n!}
Also, write
\frac{H(x)^m}{m!}=\sum_{n=1}^\infty e_n\frac {x^n}{n!}
In order to prove that
\frac{H(x)^{m+1}}{(m+1)!}=k_{m+1}(x),
it suffices to prove that
\frac{c_n}{n!}=\frac 1{m+1}\left(\sum_{j=0}^n\frac {e_j}{j!}\frac {b_{n-j}}{(n-j)!}\right)
Equivalently,
(m+1)c_n=\sum_{j=0}^n {n\choose j}e_{n-j}b_j
Consider the set of all labelled graphs with (m+1) connected components, such that one of the connected components has j vertices. There are
n\choose j
ways to choose j vertices from [n] . Once such a set of vertices is chooses, there are b_j such connected labelled graphs. On the other hand, by induction hypothesis, there are e_{n-j} labelled graphs on the other n-j vertices, having m connected components. Thus, total such graphs is
\sum_{j=0}^n {n\choose j}e_{n-j}b_j
But now, we have counted each labelled graph with m+1 components exactly m+1 times. Hence,
(m+1)c_n=\sum_{j=0}^n {n\choose j}e_{n-j}b_j
As explained, this proves that H(x)^m/m! is the exponential generating series for labeled graph with exactly m connected components.
Thus, exponential generating function of labelled graphs is
F(x)=\sum_{n=1}^\infty \frac {H(x)^m}{m!}=e^{H(x)}-1
3 Using the log-formula, we have
1+F(x)=e^{H(x)}~\Rightarrow~H(x)=\log(1+F(x))=\sum_{k=1}^\infty F(x)^k\frac{(-1)^{k+1}}{k!}

Labels: , ,

posted by ChemistryExplain @ August 04, 2020   0 Comments

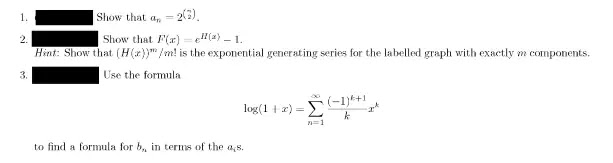
0 Comments:

Post a Comment

Subscribe to Post Comments [Atom]

<< Home