#415 Consider the differential equation xy + y - xy = 0
Consider the differential equation xy + y - xy = 0 - Math
ChemistryExplain daily providing Q&A content “#415 Consider the differential equation xy + y - xy = 0" in Bridges math curriculum, Dr mather, Carnegie math, 10th maths, 10th grade math problems, Math
Get the Free Online Chemistry Q&A Questions And Answers with explain. To crack any examinations and Interview tests these Chemistry Questions And Answers are very useful. Here we have uploaded the Free Online Chemistry Questions. Here we are also given the all chemistry topic.
ChemistryExplain team has covered all Topics related to inorganic, organic, physical chemistry, and others So, Prepare these Chemistry Questions and Answers with Explanation Pdf.
For More Chegg Questions
Free Chegg Question
Consider the differential equation,
The objective is to find the basis of solution by the Frobenius method.
Free Chegg AnswerFor More Chemistry Notes and Helpful Content Subscribe Our YouTube Chanel - Chemistry Explain
Free Chegg Answer
-
Step 1 of 10
Consider the differential equation,
The objective is to find the basis of solution by the Frobenius method.
-
Step 2 of 10
Let
. Then,
,
Substitute the above values in the equation
, get,
Separate the terms for
.
Replace
in the first and second series and
in third series.
-
Step 3 of 10
Continuation to the above step,
Compare the coefficients on both sides to get,
And,
-
Step 4 of 10
Since
yields nothing, take
Hence the indicial roots are,
.
For
the recurrence relation becomes,
And,
For
,
-
Step 5 of 10
For
,
For
,
-
Step 6 of 10
For,
For
,
And so on.
-
Step 7 of 10
Therefore, the first solution is,
That is, the solution is,
-
Step 8 of 10
Use reduction of order method to obtain the second solution.
Formula to obtain second solution of standard form,
,
as first second solution
is,
-
Step 9 of 10
write the given differential equation in standard form.
[Original equation]
standard form
Comparing it with
get
Hence the second solution of this equation is,
-
Step 10 of 10
Continuation to the above step,
Hence the second solution is,
Labels: Chegg, Free Chegg Answer, Q&A Math



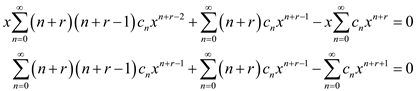









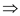




















0 Comments:
Post a Comment
Subscribe to Post Comments [Atom]
<< Home